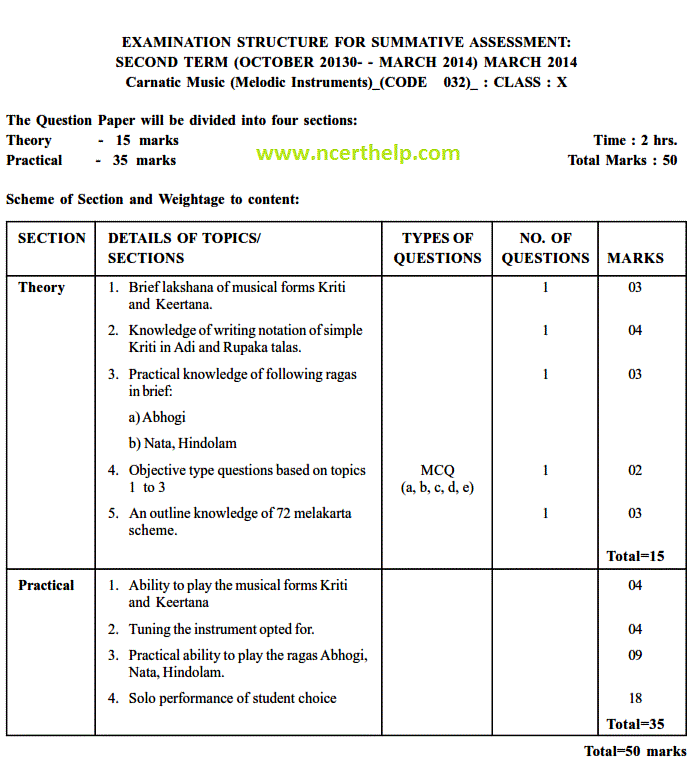
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
AnswerLet A, B, and C be the set of people who like product A, B, and C respectively.
n(A) = 21, n(B) = 26, n(C) = 29, n(A ∩ B) = 14, n(C ∩ A) = 12, n(B ∩ C) = 14, n(A ∩ B ∩ C) = 8
People who many liked product C only
= n(C) - n(C ∩ A) - n(B ∩ C) + n(A ∩ B ∩ C)
= 29 -12 – 14 + 8
= 11
Hence, 11 liked product C only.




























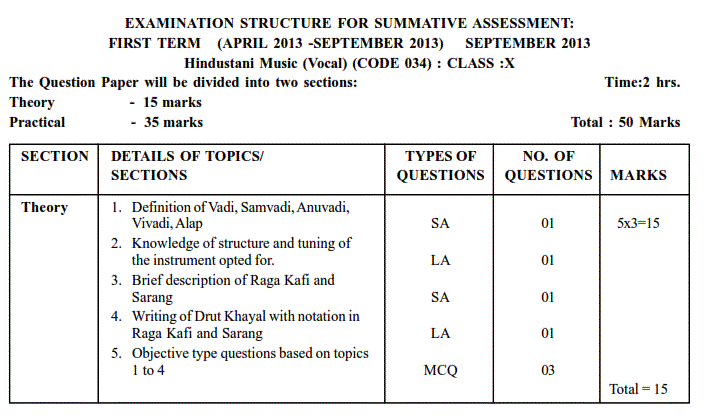


+01.gif)
+02.gif)
+01.gif)
+02.gif)
+03.gif)